For general information, see the ADCIRC site, ADCIRC FAQ, or the ADCIRC Wikipedia page. For model documentation not yet available on the wiki, see the ADCIRC site. New content is being continuously added to the ADCIRCWiki, and material from the main ADCIRC site will be gradually transitioned over to the wiki.
Generalized Asymmetric Holland Model: Difference between revisions
Luckygirl001 (talk | contribs) |
Taylorgasher (talk | contribs) m (added categories) |
||
| (10 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
<!-- markdown file for GAHM on ADCIRCWIKI--> | <!-- markdown file for GAHM on ADCIRCWIKI--> | ||
The Generalized Asymmetric Holland Model (GAHM) is a parametric hurricane vortex model developed in ADCIRC for operational forecasting purpose | The Generalized Asymmetric Holland Model (hereinafter, GAHM) is a parametric hurricane vortex model developed in ADCIRC for operational forecasting purpose, based on the classic Holland Model <ref> Holland, G. J., 1980: An analytic model of the wind and pressure profiles in hurricanes. ''Monthly Weather Review'', 108, 1212-1218. </ref> (hereinafter, HM). The original HM was developed to render an ideal symmetric hurricane (a.k.a., annular hurricane). To represent hurricanes that may exhibit asymmetric structures, the Asymmetric Holland Model (hereinafter, AHM) was developed and implemented in ADCIRC for more practical usages<ref> Mattocks, C., C. Forbes, and L. Ran, 2006: Design and implementation of a real-time storm surge and flood forecasting capability for the State of North Carolina. UNC-CEP Technical Report, University of North Carolina, 103pp. </ref>, which has the same set of equations as of the HM, but takes azimuthally-varying radius to the maximum wind to reconstruct its spatial pressure and wind fields. Both the HM and AHM suffer from flaws that make rendering large but weak storms difficult. As a result, efforts were made to develop a more generalized model to fulfill the purpose. Compared to the HM and the AHM, the GAHM removes the assumption of cyclostrophic balance at the radius of maximum wind during derivation of its equations, and allows for a better representation of a wide range of hurricanes. Another important feature of the GAHM is the introduction of a composite wind method, which when activated enables the usage of multiple storm isotaches. It makes representing complex hurricane structures possible. | ||
<!-- ********************* chapter 1 ******************* --> | <!-- ********************* chapter 1 ******************* --> | ||
== The Classic Holland Model == | == The Classic Holland Model == | ||
The | The HM is an analytic model that describes the radial pressure and wind profiles of a standard hurricane. To begin with, Holland found that the normalized pressure profiles of a number of hurricanes resemble a family of rectangular hyperbolas and may be approximated by a hyperbolic equation, which after antilogarithms and rearranging yields the radial pressure equation: | ||
<center> <math> P(r) = P_c + (P_n - P_c)e^{-A/r^B} \quad </math> (1) </center> | <center> <math> P(r) = P_c + (P_n - P_c)e^{-A/r^B} \quad </math> (1) </center> | ||
| Line 11: | Line 11: | ||
where <math> P_c </math> is the central pressure, <math> P_c </math> is the ambient pressure (theoretically at infinite radius), <math> P(r) </math> is the pressure at radius <math> r </math> from the center of the hurricane, and <math> A </math> and <math> B </math> are shape parameters that may be empirically estimated from observations in a hurricane. | where <math> P_c </math> is the central pressure, <math> P_c </math> is the ambient pressure (theoretically at infinite radius), <math> P(r) </math> is the pressure at radius <math> r </math> from the center of the hurricane, and <math> A </math> and <math> B </math> are shape parameters that may be empirically estimated from observations in a hurricane. | ||
Substituting (1) into the gradient wind equation, which describes a steady flow balanced by the horizontal pressure gradient force, the centripetal acceleration, and the Coriolis acceleration for a vortex above the influence of the planetary boundary layer where the atmospheric flow decouples from surface friction | Substituting (1) into the gradient wind equation, which describes a steady flow balanced by the horizontal pressure gradient force, the centripetal acceleration, and the Coriolis acceleration for a vortex above the influence of the planetary boundary layer where the atmospheric flow decouples from surface friction <ref> Powell, Mark & Uhlhorn, E. & Kepert, Jeffrey. (2009). Estimating Maximum Surface Winds from Hurricane Reconnaissance Measurements. ''Weather and Forecasting''. 24. 10.1175/2008WAF2007087.1. </ref>, gives the radial wind equation of a hurricane: | ||
<center> <math> V_g(r) = \sqrt{AB(P_n - P_c)e^{-A/r^B}/\rho r^B + (\frac{rf}{2})^2} - \frac{rf}{2} \quad </math> (2) </center> | <center> <math> V_g(r) = \sqrt{AB(P_n - P_c)e^{-A/r^B}/\rho r^B + (\frac{rf}{2})^2} - \frac{rf}{2} \quad </math> (2) </center> | ||
| Line 33: | Line 33: | ||
<center> <math> V_g(r) = \sqrt{(V_{max})^2e^{1-(R_{max}/r)^B}(R_{max}/r)^B + (\frac{rf}{2})^2} - \frac{rf}{2} \quad </math> (7) </center> | <center> <math> V_g(r) = \sqrt{(V_{max})^2e^{1-(R_{max}/r)^B}(R_{max}/r)^B + (\frac{rf}{2})^2} - \frac{rf}{2} \quad </math> (7) </center> | ||
When sparse observations of a hurricane are given, estimates of the <math> R_{max} </math> and shape parameter <math> B </math> can be estimated by fitting data into the radial wind equation, which in turn allow us to compute <math> P(r) </math> and <math> V_g(r) </math> along the radius <math> r </math> of the hurricane. However, discrepancies between wind observations and computed winds were sometimes found, and were negatively correlated to the Rossby number at <math> r = R_{max} </math>, defined as | |||
<center> <math> R_o = \frac{Nonlinear Acceleration}{Coriolis force} | <center> <math> R_o = \frac{Nonlinear Acceleration}{Coriolis force} \approx \frac{V_{max}^2/R_{max}}{V_{max}f} = \frac{V_{max}}{R_{max}f} \quad </math> (8) </center> | ||
By definition, a large <math> R_o (\approx 10^3) </math> describes a system in cyclostrophic balance that is dominated by the inertial and centrifugal force with negligible Coriolis force, such as a tornado or the inner core of an intense hurricane, whereas a small value <math> (\approx 10^{-2} \sim 10^2) </math> signifies a system in geostrophic balance where the Coriolis force plays an important role, such as the outer region of a hurricane. As a result, the assumption of cyclostrophic balance at <math> R_{max} </math> made in HM is mostly valid for describing an intense and narrow (small <math> R_{max} </math>) hurricane with a large <math> R_o </math>, but not applicable for a weak and broad hurricane with a small <math> R_o </math>. This intrinsic problem with the HM calls our intention to develop a generalized model that will work consistently for a wide range of hurricanes, which theoretically can be accomplished by removing the above cyclostrophic balance assumption and re-derive the radial pressure and wind equations (6)&(7). | By definition, a large <math> R_o (\approx 10^3) </math> describes a system in cyclostrophic balance that is dominated by the inertial and centrifugal force with negligible Coriolis force, such as a tornado or the inner core of an intense hurricane, whereas a small value <math> (\approx 10^{-2} \sim 10^2) </math> signifies a system in geostrophic balance where the Coriolis force plays an important role, such as the outer region of a hurricane. As a result, the assumption of cyclostrophic balance at <math> R_{max} </math> made in HM is mostly valid for describing an intense and narrow (small <math> R_{max} </math>) hurricane with a large <math> R_o </math>, but not applicable for a weak and broad hurricane with a small <math> R_o </math>. This intrinsic problem with the HM calls our intention to develop a generalized model that will work consistently for a wide range of hurricanes, which theoretically can be accomplished by removing the above cyclostrophic balance assumption and re-derive the radial pressure and wind equations (6)&(7). | ||
| Line 42: | Line 42: | ||
== Derivation of the GAHM == | == Derivation of the GAHM == | ||
The GAHM also starts with the same radial pressure and wind equations (1)&(2) with shape parameters <math> A </math> and <math> B </math> as in the HM. Without assuming cyclostrophic balance at <math> R_{max} </math>, we take <math> dV_g/dr = 0 </math> at <math> r = R_{max} </math> to get the adjusted shape parameter <math> B_g </math> as | The GAHM also starts with the same radial pressure and wind equations (1)&(2) with shape parameters <math> A </math> and <math> B </math>, as in the HM. Without assuming cyclostrophic balance at <math> R_{max} </math>, we take <math> dV_g/dr = 0 </math> at <math> r = R_{max} </math> to get the adjusted shape parameter <math> B_g </math> as | ||
<center> <math> B_g = \frac{(V_{max}^2 + V_{max}R_{max}f)\rho e^\varphi}{\varphi(P_n - P_c)} = B \frac{(1+1/R_o)e^{\varphi - 1}}{\varphi} \quad </math> (9) </center> | <center> <math> B_g = \frac{(V_{max}^2 + V_{max}R_{max}f)\rho e^\varphi}{\varphi(P_n - P_c)} = B \frac{(1+1/R_o)e^{\varphi - 1}}{\varphi} \quad </math> (9) </center> | ||
| Line 57: | Line 57: | ||
[[File:Fig 1. GAHM.png|center|Profiles of Bg⁄B (left panel) and φ (right panel)]] | [[File:Fig 1. GAHM.png|center|Profiles of Bg⁄B (left panel) and φ (right panel)]] | ||
<center> | <center> Figure 1. Profiles of <math> B_g/B </math> (left panel) and <math> \varphi </math> (right panel) with respect to <math> \log_{10}R_o </math>, given different <math> B </math> values as shown in different colors. </center> | ||
Substituting (9)&(11) back into (1)&(2) yields the final radial pressure and wind equations for the GAHM | Substituting (9)&(11) back into (1)&(2) yields the final radial pressure and wind equations for the GAHM | ||
| Line 71: | Line 71: | ||
[[File:Fig 2. GAHM.png|center|Comparison of the normalized gradient winds]] | [[File:Fig 2. GAHM.png|center|Comparison of the normalized gradient winds]] | ||
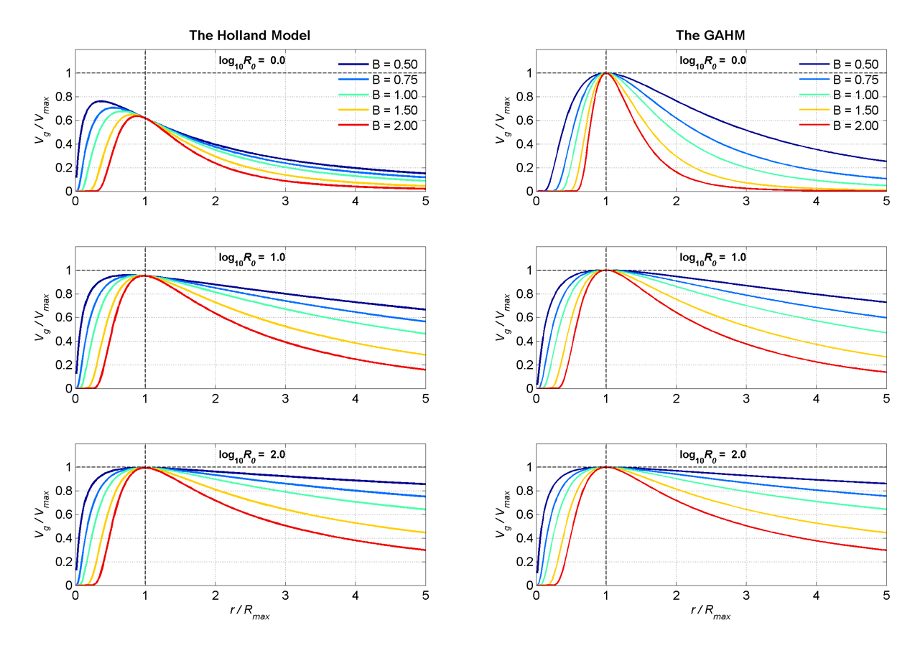
<center> | <center> Figure 2. The normalized gradient wind profiles of the HM (left panel) and the GAHM (right panel) as functions of the normalized radial distances and <math> \log_{10}R_o </math>, given different Holland <math> B </math> values. </center> | ||
To have a dissective look of the surface plots in Figure 2, we draw slices perpendicular to the axis of <math> \log_{10}R_o </math> at three different values 0, 1, 2, and plot the lines of intersection with each surface in Figure 3. It is evident that we get <math> V_g = V_{max} </math> at <math> r = R_{max} </math> consistently in the right panel for the GAHM regardless of the value of <math> R_o </math>. The HM in the left panel, however, generates distorted wind profiles with underestimated maximum winds skewed inward towards the storm center, espeically when <math> \log_{10}R_o < 1 </math>. As a results, when both models being applied to real hurricane cases, the GAHM will perform more consistently than the HM. | To have a dissective look of the surface plots in Figure 2, we draw slices perpendicular to the axis of <math> \log_{10}R_o </math> at three different values 0, 1, 2, and plot the lines of intersection with each surface in Figure 3. It is evident that we get <math> V_g = V_{max} </math> at <math> r = R_{max} </math> consistently in the right panel for the GAHM regardless of the value of <math> R_o </math>. The HM in the left panel, however, generates distorted wind profiles with underestimated maximum winds skewed inward towards the storm center, espeically when <math> \log_{10}R_o < 1 </math>. As a results, when both models being applied to real hurricane cases, the GAHM will perform more consistently than the HM. | ||
| Line 79: | Line 79: | ||
<!-- ********************* chapter 3 ******************* --> | <!-- ********************* chapter 3 ******************* --> | ||
== Calculation of the Radius to the Maximum Wind == | == Calculation of the Radius to the Maximum Wind == | ||
Same with the HM and AHM, the GAHM also uses processed forecast advisories (during active hurricanes) or best track advisories (post-hurricanes) from the National Hurricane Center (NHC) in ATCF format as input files, which contain a time series of storm parameters (usually at 6-hour intervals) such as storm location, storm movement, central pressure, 1 minute averaged maximum wind, radii to the 34-, 50-, and/or 64-kt storm isotaches in 4 storm quadrants (NE, SE, SW, NW), etc. See meteorological input file with NWS = 20 for more details. As a standard procedure, the <math> B_g </math> and <math> R_{max} </math> are pre-computed in 4 storm quadrants for all available isotaches in the ASWIP program <ref group = "footnotes"> The auxiliary preprocessing program ASWIP.F (located in the /wind directory) was further developed here to accommodate the GAHM. </ref> and appended to the input file prior to running an ADCIRC simulation. The following describes the procedures to prepare the input file for the GAHM. | |||
First, the influence of the boundary layer effect must be removed to bring the maximum sustained wind and the 34-, 50-, and/or 64-kt isotaches from 10 meter height to the gradient wind level. Practically, the maximum gradient wind can be directly calculated as | First, the influence of the boundary layer effect must be removed to bring the maximum sustained wind and the 34-, 50-, and/or 64-kt isotaches from 10 meter height to the gradient wind level. Practically, the maximum gradient wind can be directly calculated as | ||
| Line 89: | Line 89: | ||
<center> <math> V_{max} = \vert \frac{\overrightarrow{V_M} - \gamma\overrightarrow{V_T}}{W_{rf}} \vert = \frac{V_M - \gamma V_T}{W_{rf}} \quad </math> (14) </center> | <center> <math> V_{max} = \vert \frac{\overrightarrow{V_M} - \gamma\overrightarrow{V_T}}{W_{rf}} \vert = \frac{V_M - \gamma V_T}{W_{rf}} \quad </math> (14) </center> | ||
where <math> \overrightarrow{V_M} </math> is the reported maximum sustained wind at 10 meter height assuming in the same direction as <math> \overrightarrow{V_T} </math>, <math> \overrightarrow{V_T} </math> is the storm translational speed calculated from successive storm center locations, <math> W_{rf} = 0.9 </math> is the wind reduction factor for reducing wind speed from the gradient wind level to the surface at 10 meter height (Powell et al., 2003), and <math> \gamma </math> is the damp factor for <math> V_T </math>. The following formula of <math> \gamma </math> is | where <math> \overrightarrow{V_M} </math> is the reported maximum sustained wind at 10 meter height assuming in the same direction as <math> \overrightarrow{V_T} </math>, <math> \overrightarrow{V_T} </math> is the storm translational speed calculated from successive storm center locations, <math> W_{rf} = 0.9 </math> is the wind reduction factor for reducing wind speed from the gradient wind level to the surface at 10 meter height (Powell et al., 2003), and <math> \gamma </math> is the damp factor for <math> V_T </math>. The following formula of <math> \gamma </math> is employed in the ASWIP program: | ||
<center> <math> \gamma = \frac{V_g}{V_{max}} \quad </math> (15) </center> | <center> <math> \gamma = \frac{V_g}{V_{max}} \quad </math> (15) </center> | ||
| Line 95: | Line 95: | ||
which is the ratio of gradient wind speed to the maximum wind speed along a radial wind profile. Thus, <math> \gamma </math> is zero at storm center, and increases with <math> r </math> until reaches a maximum value of 1 at <math> R_{max} </math>, then gradually decreases outward to zero. | which is the ratio of gradient wind speed to the maximum wind speed along a radial wind profile. Thus, <math> \gamma </math> is zero at storm center, and increases with <math> r </math> until reaches a maximum value of 1 at <math> R_{max} </math>, then gradually decreases outward to zero. | ||
In addition to the scalar reduction in wind speed, surface friction and continuity also cause the vortex wind to flow inward across isobars, with an inward rotation angle <math> \beta </math> according to the Queensland Government's Ocean Hazards Assessment (2001): | In addition to the scalar reduction in wind speed, surface friction and continuity also cause the vortex wind to flow inward across isobars, with an inward rotation angle <math> \beta </math> according to the Queensland Government's Ocean Hazards Assessment (2001) <ref> Queensland Government, 2011: Queensland Climate Change and Community Vulnerability to Tropical Cyclone, ''Ocean Hazards Assessment – Stage 1''. </ref>: | ||
<center> <math> \beta = \begin{cases} | <center> <math> \beta = \begin{cases} | ||
| Line 109: | Line 109: | ||
& = \frac{\vert\overrightarrow{V_{isot}} - \gamma\overrightarrow{V_T} \vert}{W_{rf}} | & = \frac{\vert\overrightarrow{V_{isot}} - \gamma\overrightarrow{V_T} \vert}{W_{rf}} | ||
\end{align} \quad </math> (17) </center> | \end{align} \quad </math> (17) </center> | ||
where <math> \overrightarrow{V_{isot}} </math> is the observed isotach wind speed with an unknown angle <math> \varepsilon </math>, and <math> \overrightarrow{V_{inflow}} </math> is the wind speed at radius to specified isotach before the inward rotation angle <math> \beta </math> is removed. | where <math> \overrightarrow{V_{isot}} </math> is the observed isotach wind speed with an unknown angle <math> \varepsilon </math>, and <math> \overrightarrow{V_{inflow}} </math> is the wind speed at radius to specified isotach before the inward rotation angle <math> \beta </math> is removed. | ||
| Line 135: | Line 133: | ||
== Composite Wind Generation == | == Composite Wind Generation == | ||
Since storm parameters are only given in 4 storm quadrants (assuming at <math> 45^\circ, 135^\circ, 225^\circ, 315^\circ </math> azimuthal angles, respectively) at 3 available isotaches in the input file, spatial interpolation of storm parameters must take place first at each ADCIRC grid node. Traditionally, the single-isotach approach is used by the AHM, in which storm parameters will be interpolated azimuthally from the highest isotach only. To take advantage of the availability of multiple isotaches, a new composite wind method is introduced in the GAHM, the multiple-isotach approach, in which storm parameters will be interpolated both azimuthally and radially from all available isotaches. | |||
| Line 157: | Line 155: | ||
and <math> f_{34}+f_{50}+f_{64}=1 </math>. | and <math> f_{34}+f_{50}+f_{64}=1 </math>. | ||
The above procedure is performed at each node of an ADCIRC grid | The above procedure is performed at each node of an ADCIRC grid. After all storm parameters are interpolated, the pressure and gradient winds can be calculated using (12)&(13). To bring the gradient wind down to the standard 10 meter reference level, the same wind reduction factor <math> W_{rf} </math> is applied, and the tangential winds are rotated by an inward flow angle β according to (16). Then, the storm translational speed is added back to the vortex winds. Last but not least, a wind averaging factor is applied to convert resulted wind field from 1-min to 10-min averaged winds in order to be used by ADCIRC. This new composite wind method is simple and efficient, and more importantly, it assures that the constructed surface winds match all observed storm isotaches provided in NHC’s forecast or “best track” advisories. | ||
<!-- ********************* chapter 5 ******************* --> | |||
== Case Studies == | |||
Preliminary evaluation of the GAHM was carried out based on seven hurricanes that struck the Gulf of Mexico and the Eastern United States: Katrina (2005), Rita (2005), Gustav (2008), Ike (2008), Irene (2011), Isaac (2012), and Sandy (2012), see Table 1. Ranging from category 1 to 5 on the Saffir-Simpson Hurricane Wind Scale, these storms vary in storm track, forward motion, size, intensity, and duration, but all caused severe damages to coastal states due to destructive winds, wind-induced storm surges, and ocean waves. Their “best track” advisories were retrieved from NHC’s ftp site (ftp://ftp.nhc.noaa.gov/atcf; previous years’ data are located in the archive directory) and pre-processed using the ASWIP program. The “best track” file contains an estimate of the radius to the maximum wind for each data entry, but will solely be used for model validation purpose as both the GAHM and AHM calculate their own spatially-varying <math> R_{max} </math>. | |||
{| class="wikitable" style="text-align:center" style="margin: 1em auto 1em auto" | |||
|+'''Table 1. Seven selected hurricanes used for preliminary evaluation of the GAHM''' | |||
|- | |||
! Hurricane !! Saffir-Simpson Wind Scale !! Maximum Sustained Wind (knot) !! Minimum Central Pressure (mbar) !! Period from Formation to Dissipation | |||
|- | |||
| '''Katrina''' || 5 || 150 || 902 || 08/23-08/30, 2005 | |||
|- | |||
| '''Rita''' || 5 || 150 || 902 || 09/18-09/26, 2005 | |||
|- | |||
| '''Gustav''' || 4 || 135 || 941 || 08/23-09/04, 2008 | |||
|- | |||
| '''Ike''' || 4 || 125 || 935 || 09/01-09/14, 2008 | |||
|- | |||
| '''Irene''' || 3 || 105 || 942 || 08/21-08/30, 2011 | |||
|- | |||
| '''Isaac''' || 1 || 70 || 965 || 08/21-09/03, 2012 | |||
|- | |||
| '''Sandy''' || 3 || 95 || 940 || 10/22-10/01, 2012 | |||
|} | |||
Besides the maximum wind speed, both Holland <math> B </math> and <math> R_o </math> can be used as key storm characteristics to characterize the development of the storm. Figure 4 depicts the change of <math> V_M </math>, <math> B </math>, and <math> \log_{10}R_o </math> during different stages of the hurricanes along their best tracks. Typically, both <math> B </math> and <math> R_o </math> increase as hurricane strengthens, and decrease as hurricane dissipates, within the range of (0, 2.5). Previous analytical evaluation has demonstrated that the GAHM behaves consistently better than the HM, especially under situations where <math> \log_{10}R_o < 1 </math>. Here, evaluation of model performance will be carried out by comparing the modeled winds with the observed winds in the "best track" data, as well as the AHM, the SLOSH (Sea, Lake, and Overland Surges from Hurricanes) winds, re-analysis H*Wind and hindcast OWI modeled winds. The OWI winds and H*Winds are considered more mature wind products that are able to resolve more complex structures of a hurricane than the simple vortex models do. | |||
{| border="0" cellpadding="5" cellspacing="0" align="center" | |||
|- | |||
| align="center" width="33%" | [[File:Fig 4. GAHM.png|360px]] | |||
| align="center" width="33%" | [[File:Fig 5. GAHM.png|360px]] | |||
| align="center" width="33%" | [[File:Fig 6. GAHM.png|360px]] | |||
|- | |||
| colspan="3" align="center" |Figure 4. The development of (a) The Maximum Wind Speed, (b) Holland <math> B </math>, and (c) <math> \log_{10}R_o </math> along the best tracks of 7 selected hurricanes | |||
|} | |||
<!-- subsection I --> | |||
<!-- Demonstrate the improvements made in the GAHM over the original HM --> | |||
=== The AHM vs. The GAHM === | |||
* '''Comparison of Radial Wind Profiles using the Single-Isotach Approach''' | |||
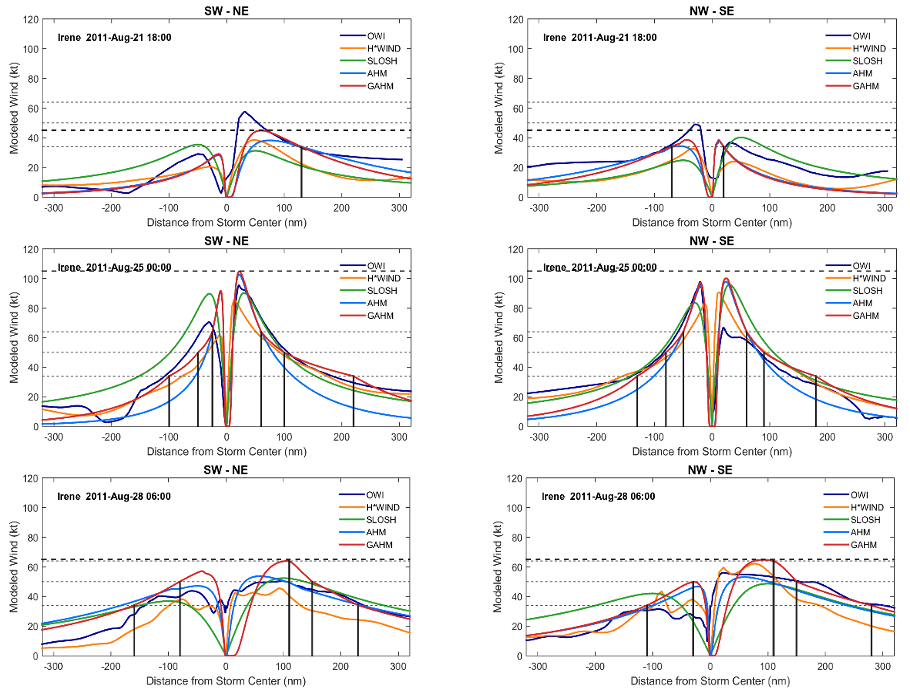
Since the AHM is an advanced version of the HM, here we only use model results from the AHM for comparisons with the GAHM. First, the single-isotach approach was evaluated using Hurricane Irene (2011) as an example. Figure 5 gives the comparison of radial wind profiles of Hurricane Irene (2011) between the AHM and the GAHM using the single-isotach approach at three snapshots, each representing the developing (top panels), mature (middle panels), and dissipating (bottom panels) stages of the hurricane. | |||
[[File:Fig 7. GAHM.png|center|Radial wind profiles of Irene (2011) at three different stages.]] | |||
<center> Figure 5. Comparison of radial wind profiles of Irene (2011) at three different stages between the AHM and the GAHM. </center> | |||
The cross-section radial winds from SW to NE are given in the left panels, and NW to SE in the right panels. The observed isotaches at radii to specified isotaches given in the "best track" file are also plotted as vertical line segments for reference (highest isotach in black and lower isotaches in gray). For a perfect match between the modeled winds and the isotaches, the radial profiles should meet the tip of the line segments at the exact same height. The <math> B </math>, <math> B_g </math> and <math> \log_{10}R_o </math> are also computed at the same snapshots in all 4 quadrants, given by Table 2. | |||
{| class="wikitable" style="text-align:center" style="margin: 1em auto 1em auto" width = "75%" | |||
|+'''Table 2. Key storm characteristics <math> B </math>, <math> B_g </math> and <math> \log_{10}R_o </math> at three snapshots of Irene (2011)''' | |||
| | |||
! colspan="4" | 2011-Aug-21 18:00 | |||
! colspan="4" | 2011-Aug-25 00:00 | |||
! colspan="4" | 2011-Aug-28 06:00 | |||
|- | |||
| '''Quadrant''' || NE || SE || SE || NW || NE || SE || SW || NW ||NE || SE || SW || NW | |||
|- | |||
| '''<math> \boldsymbol{B} </math> '''|| 1.00 || 1.00 || 1.00 || 1.00 || 1.62 || 1.62 || 1.62 || 1.62 || 0.60 || 0.60 || 0.60 || 0.60 | |||
|- | |||
| '''<math> \boldsymbol{B_g} </math> '''|| 1.24 || 1.03 || 1.05 || 1.19 || 1.69 || 1.69 || 1.65 || 1.68 || 1.11 || 0.92 || 0.72 || 0.73 | |||
|- | |||
| '''<math> \boldsymbol{log_{10}R_o} </math> '''|| 0.64 || 1.44 || 1.26 || 0.74 || 1.37 || 1.36 || 1.70 || 1.41 || 0.28 || 0.33 || 0.74 || 0.82 | |||
|} | |||
It is evident that the radial wind profiles generated by the GAHM consistently match the highest isotaches in all quadrants at different stages of Irene, no matter how <math> B </math> and <math> \log_{10}R_o </math> vary. The AHM did a similarly good job when the hurricane is strong (see middle panels), but failed to match the highest isotaches when <math> \log_{10}R_o < 1 </math>. Both the AHM and the GAHM winds died off too quickly away from the storm center, thus failed to match any lower isotaches. | |||
* '''Evaluation of the Maximum Winds and Radius to Maximum Winds''' | |||
Comparisons of the modeled maximum winds and radius to maximum winds to the observed values in the input file were also carried out based on all 7 selected hurricanes, given by the scatter plots in Figure 6. Evaluations of the maximum winds are given in the upper panels, while the radius to maximum winds given in lower panels, both color-coded by <math> \log_{10}R_o </math>, with a simple linear correlation given in each panel. Examination of the upper panels reveals that the GAHM did an excellent job in estimating the maximum winds, with a few overestimations near the lower bound of the dataset. Careful examinations of these over estimated values revealed that they were from those "bad" dada entries in the "best track" file that violate certain criteria in the GAHM when solving for the <math> R_{max} </math>. This phenomenon was particular common during the dissipating stage of a hurricane. The AHM had larger discrepancies in estimating the maximum wind compared to the GAHM, especially when <math> \log_{10}R_o < 1 </math>, which was a direct consequence of the cyclostrophic balance assumption made during the derivation of HM's equations. Examination of the lower panels reveals that the maximum value of the modeled azimuthally-varying <math> R_{max} </math> failed to match the observed <math> R_{max} </math> values given in the input file, but the trend of the GAHM was significantly better. | |||
{| border="0" cellpadding="5" cellspacing="0" align="center" | |||
|- | |||
| align="center"|[[File:Fig 8.1. GAHM.png|800px]] | |||
|- | |||
| align="center"|[[File:Fig 8.2. GAHM.png|800px]] | |||
|- | |||
| align="center"|Figure 6. Comparison of the modeled and “Best Track” maximum winds (upper two panels), and the modeled and “Best Track” <math> R_{max} </math> (lower two panels) between the AHM and the GAHM based on all seven hurricanes. | |||
|} | |||
* '''Demonstration of the Multiple-Isotach Approach''' | |||
Earlier we have shown that a radial wind profile constructed by the GAHM using the single-isotach approach would only match the highest isotach, due to limitations of this single-fitting method. In fact, underestimations of modeled winds at distances to isotachs other than the highest one were common, as the radial wind profile tends to die off too quickly away from the storm center due to the nature of GAHM’s formulas. In an effort to minimize the combined errors mentioned above, and to improve the overall accuracy of the estimated wind field, the multiple-isotach approach should be used whenever there is more than one isotach present in the best track file. | |||
The 3D plots of Irene’s radial wind profiles (left) and interpolated spatial wind fields (right) by the GAHM using the single-isotach approach (upper panels) versus the multiple-isotach approach (lower panels) were given by Figure 7. For easier visualization, all available isotaches were plotted at radii to specified isotaches in the left two panels, and as contour lines (after azimuthal interpolation) in the right two panels. It is evident that winds generated by the multiple-isotach approach were able to match all given isotaches in all 4 quadrants, while only the highest isotach was matched by the single-isotach approach. Comparison of the spatial wind fields also indicated that the multiple-isotach approach allowed the wind to die off more gradually away from the storm center than the single-isotach approach did, demonstrated by the smaller gradient of the contour lines in the lower panel. It is believed that the multiple-isotach approach improves the overall accuracy and performance of the GAHM. | |||
[[File:Fig 9. GAHM.png|center|800px|Irene’s radial wind profiles (left) and interpolated spatial wind field (right)]] | |||
<center> Figure 7. 3D plot of Irene’s radial wind profiles (left) and interpolated spatial wind fields (right) by the single-isotach approach (upper panels) and the multiple-isotach approach (lower panels). </center> | |||
<!-- subsection II --> | |||
<!-- Compare the GAHM's composite wind field with other wind products --> | |||
=== Evaluation of GAHM's Composite Wind Field === | |||
* '''Comparison of Radial Wind Profiles''' | |||
Using the multiple-isotach approach, radial wind profiles generated from the GAHM were compared to those from the AHM, the SLOSH, H*Winds, and OWI winds, shown in Figure 8 at three different stages of Irene (2011), with the left panels showing the SW to NE cross-section winds, and the right showing the NW to SE cross-section winds (same as in Figure 5). It is evident that the GAHM's composite radial wind profiles matched all available storm isotachs at all time, while the rest of the models failed most of the time. The SLOSH model, which is also a parametric wind model, does not take the isotach information to construct its wind field, so generally did a bad job matching any given isotaches. More detailed wind structures can be observed from the radial profiles extracted from the H*Wind and OWI winds than those from the parametric wind profiles, as expected. However, profiles from different models in general did not match each other due to different mechanisms involved in each model. | |||
[[File:Picture12 GAHM.png|center|Comparison of radial wind profiles of Irene (2011)]] | |||
<center> Figure 8. Comparison of radial wind profiles of Irene (2011) at three different stages among the AHM, the GAHM, SLOSH, H*Wind and OWI winds. </center> | |||
* '''Evaluation of Model Results at Radii to Given Isotaches''' | |||
<!-- statistics --> | |||
[[File:Picture13 GAHM.png|center|Comparison of specified isotachs and modeled winds]] | |||
<center> Figure 9. Evaluation of modeled wind at radii to given isotaches based on all seven selected storms. </center> | |||
Quantitative evaluation of the GAHM's performance at radii to given isotaches were given in Figure 9, with statistics given in Table 3, based on all seven selected hurricanes. The GAHM had almost perfect match to each of the 34-, 50-, and 64-kt isotaches, with a standard deviation around 0.1 kt, which was very impressive. The AHM matched the 64-kt isotach reasonably well with a mean of 63.3 kts, but failed at the lower isotaches. The SLOSH did not take any isotach information to construct its wind fields, thus behaved poorly in matching any given isotaches. Its data also had the largest spread compared to other models, with standard deviation ranging from 11 to 16 kts. For the H*Wind and the OWI winds, the means of modeled winds were close to each specified isotach, generally within ±3 kts, but the spreads of data were also large compared to that of the AHM and the GAHM, with a standard deviation greater than 7 kts. | |||
{| class="wikitable" style="text-align:center" style="margin: 1em auto 1em auto" width = "75%" | |||
|+'''Table 3. Statistical analysis of modeled winds at radii to specified isotaches based on all seven storms''' | |||
| | |||
! colspan="3" | MEAN (kt) | |||
! colspan="3" | Standard Deviation (kt) | |||
|- | |||
| | |||
| Iso-34 || Iso-50 || Iso-64 || Iso-34 || Iso-50 || Iso-64 | |||
|- | |||
| '''AHM''' || 26.9 || 44.7 || 63.3 || 7.96 || 7.09 || 2.55 | |||
|- | |||
| '''GAHM''' || 34.0 || 50.0 || 64.0 || 0.10 || 0.12 || 0.10 | |||
|- | |||
| '''SLOSH''' || 30.0 || 48.9 || 69.5 || 11.00 || 14.11 || 16.08 | |||
|- | |||
| '''OWI''' || 33.1 || 48.3 || 61.3 || 7.65 || 8.71 || 9.42 | |||
|- | |||
| '''H*Wind''' || 34.9 || 49.2 || 61.2 || 7.55 || 8.88 || 8.89 | |||
|} | |||
* '''Comparison of Spatial Wind fields''' | |||
<!-- spatial plots among 5 models --> | |||
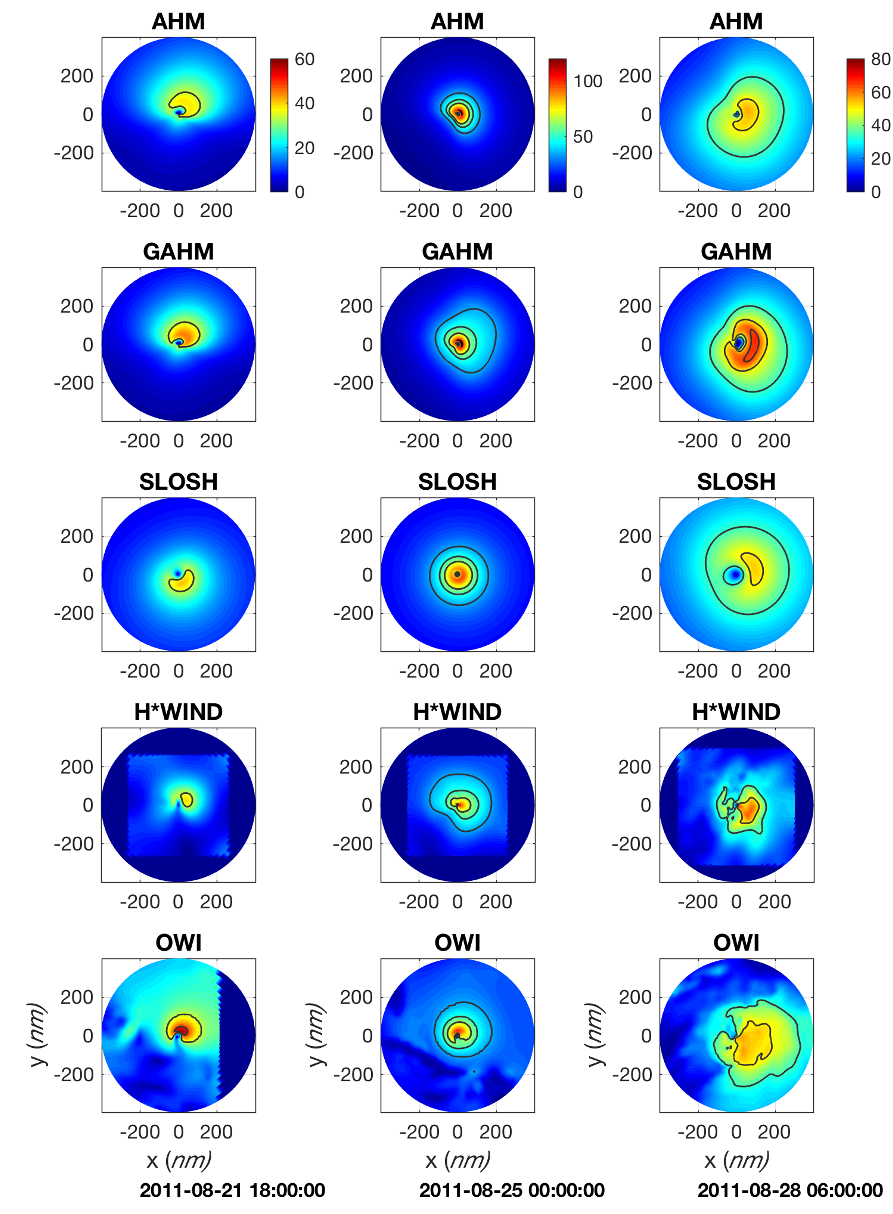
Comparisons of spatial wind fields among the AHM, the GAHM using the multiple-isotach approach, the SLOSH, H*Wind and OWI winds (in rows) were given by Figure 10 at the same snapshots (in columns) as in Figure 8. The 34-, 50-, and 64-kt contour lines were shown in each wind snapshot. In general, the AHM and GAHM winds shared a lot of similarities. During weaker periods of Irene, the differences between the AHM and the GAHM's spatial wind fields were mostly observed in the inner region of the hurricane due to differences in calculated <math> R_{max} </math>. More specifically, the calculated <math> R_{max} </math> in the AHM was under-predicted (thus is closer to the storm center) than that in the GAHM, resulted from the faulty cyclostrophic balance assumption made in the HM and AHM. During stronger periods of Irene, however, the differences were mostly observed in the outer region of the hurricane due to the usage of the multiple-isotach approach in the GAHM. Without taking into account storm information from lower isotaches, the AHM winds tended to die off too quickly away from the storm center. The SLOSH winds did not show much similarity to the AHM and GAHM winds. It used an azimuthally constant <math> R_{max} </math> from the "best track" file to generate its vortex winds, and a distance-weighted translational speed to account for storm asymmetry, which was not rendered properly when the storm was strong. The winds fields of H*Wind and OWI winds were much more complex than those of the simple parametric models, but the GAHM did a relatively good job matching the spatial patterns of the hurricane. Although it is unlikely that the parametric winds constructed over a minimum set of data would match the level of details and complexity in the re-analysis H*Wind and the numerical OWI winds, the ability of a the GAHM to produce reasonable estimates of surface wind fields in a timely manner was highly desirable for real-time forecasting. | |||
[[File:Fig 10. GAHM.png|center|Three snapshots (in columns) of Irene’s two-dimensional wind fields by the AHM, GAHM, SLOSH, H*Wind and OWI winds]] | |||
<center> Figure 10. Comparison of Irene’s spatial wind fields by the AHM, GAHM, SLOSH, H*Wind and OWI winds at three different stages </center> | |||
== Notes == | |||
<references group = "footnotes" /> | |||
== References == | |||
<references /> | |||
[[Category:physics]] | |||
[[Category:meteorology]] | |||
Latest revision as of 13:11, 12 May 2020
The Generalized Asymmetric Holland Model (hereinafter, GAHM) is a parametric hurricane vortex model developed in ADCIRC for operational forecasting purpose, based on the classic Holland Model [1] (hereinafter, HM). The original HM was developed to render an ideal symmetric hurricane (a.k.a., annular hurricane). To represent hurricanes that may exhibit asymmetric structures, the Asymmetric Holland Model (hereinafter, AHM) was developed and implemented in ADCIRC for more practical usages[2], which has the same set of equations as of the HM, but takes azimuthally-varying radius to the maximum wind to reconstruct its spatial pressure and wind fields. Both the HM and AHM suffer from flaws that make rendering large but weak storms difficult. As a result, efforts were made to develop a more generalized model to fulfill the purpose. Compared to the HM and the AHM, the GAHM removes the assumption of cyclostrophic balance at the radius of maximum wind during derivation of its equations, and allows for a better representation of a wide range of hurricanes. Another important feature of the GAHM is the introduction of a composite wind method, which when activated enables the usage of multiple storm isotaches. It makes representing complex hurricane structures possible.
The Classic Holland Model
The HM is an analytic model that describes the radial pressure and wind profiles of a standard hurricane. To begin with, Holland found that the normalized pressure profiles of a number of hurricanes resemble a family of rectangular hyperbolas and may be approximated by a hyperbolic equation, which after antilogarithms and rearranging yields the radial pressure equation:
where is the central pressure, is the ambient pressure (theoretically at infinite radius), is the pressure at radius from the center of the hurricane, and and are shape parameters that may be empirically estimated from observations in a hurricane.
Substituting (1) into the gradient wind equation, which describes a steady flow balanced by the horizontal pressure gradient force, the centripetal acceleration, and the Coriolis acceleration for a vortex above the influence of the planetary boundary layer where the atmospheric flow decouples from surface friction [3], gives the radial wind equation of a hurricane:
where is the gradient wind at radius , is the density of air, is the Coriolis parameter. In the region of the maximum winds, if we assume that the Coriolis force is negligible in comparison to the pressure gradient and centripetal force, then the air is in cyclostrophic balance. By removing the Coriolis term in (2) we get the cyclostrophic wind
By setting at radius to the maximum wind , it is obtained that
Thus the () is irrelevant to the relative value of ambient and central pressures, and is solely defined by the shape parameters and . Substituting (4) back into (3) to get rid of , we get an estimate of as a function of the maximum wind speed
It was notable that the maximum wind speed is proportional to the square root of and irrespective of the (), given a constant pressure drop. It was also reasoned by Holland that a plausible range of would be between 1 and 2.5 for realistic hurricanes. Substituting (4) and (5) back into (1) and (2) yields the final radial pressure and wind profiles for the HM
When sparse observations of a hurricane are given, estimates of the and shape parameter can be estimated by fitting data into the radial wind equation, which in turn allow us to compute and along the radius of the hurricane. However, discrepancies between wind observations and computed winds were sometimes found, and were negatively correlated to the Rossby number at , defined as
By definition, a large describes a system in cyclostrophic balance that is dominated by the inertial and centrifugal force with negligible Coriolis force, such as a tornado or the inner core of an intense hurricane, whereas a small value signifies a system in geostrophic balance where the Coriolis force plays an important role, such as the outer region of a hurricane. As a result, the assumption of cyclostrophic balance at made in HM is mostly valid for describing an intense and narrow (small ) hurricane with a large , but not applicable for a weak and broad hurricane with a small . This intrinsic problem with the HM calls our intention to develop a generalized model that will work consistently for a wide range of hurricanes, which theoretically can be accomplished by removing the above cyclostrophic balance assumption and re-derive the radial pressure and wind equations (6)&(7).
Derivation of the GAHM
The GAHM also starts with the same radial pressure and wind equations (1)&(2) with shape parameters and , as in the HM. Without assuming cyclostrophic balance at , we take at to get the adjusted shape parameter as
where is a scaling parameter introduced to simplify the derivation process, defined as
and later derived as
Thus, the in the GAHM is not entirely defined by the shape parameters and as in the HM, but also by the scaling factor , as Equation (11) indicates that . Numerical solutions for and can be solved iteratively in the model using Equation (9)&(11). Figure 1 illustrates how and vary with given different values. It is evident that values of both and remain close to 1 when is within the range of [1,2], but increase noticeably as decreases below 1, and the smaller the value of , the bigger the changes.
Substituting (9)&(11) back into (1)&(2) yields the final radial pressure and wind equations for the GAHM
Influence of the Coriolis force on the radial pressure and wind profiles are evidenced by the presence of and in (12)&(13). A special case scenario is when we set , which corresponds to an infinitely large , then (12)&(13) in the GAHM reduce to (6)&(7) in the HM. However,for a hurricane with a relatively small , the influence of the Coriolis force can only be addressed by the GAHM. It meets our expectation that the GAHM’s solution approaches to that of the HM’s when the influence of Coriolis force is small, but departs from it when the Coriolis force plays an important role in the wind system.
The above reasoning can be demonstrated by the 3D plots in Figure 2, which show the normalized gradient winds of the HM (left panel) and the GAHM (right panel) as functions of the normalized radial distances , the Holland parameter, and . In both panels, each colored surface represents the normalized gradient winds corresponding to a unique Holland B value. By definition, we get at , which means all the surfaces in each panel should intersect with the plane of on the plane of , no matter what values of . However, the line of intersection (shown by the black line) shown in the left panel deviates from the plane of as decreases from 2 to close to 0 ( decreases from 100 to 1), while remains on the plane regardless of how changes in the right panel, demonstrating that the GAHM is mathematically more coherent than the HM.
To have a dissective look of the surface plots in Figure 2, we draw slices perpendicular to the axis of at three different values 0, 1, 2, and plot the lines of intersection with each surface in Figure 3. It is evident that we get at consistently in the right panel for the GAHM regardless of the value of . The HM in the left panel, however, generates distorted wind profiles with underestimated maximum winds skewed inward towards the storm center, espeically when . As a results, when both models being applied to real hurricane cases, the GAHM will perform more consistently than the HM.
Calculation of the Radius to the Maximum Wind
Same with the HM and AHM, the GAHM also uses processed forecast advisories (during active hurricanes) or best track advisories (post-hurricanes) from the National Hurricane Center (NHC) in ATCF format as input files, which contain a time series of storm parameters (usually at 6-hour intervals) such as storm location, storm movement, central pressure, 1 minute averaged maximum wind, radii to the 34-, 50-, and/or 64-kt storm isotaches in 4 storm quadrants (NE, SE, SW, NW), etc. See meteorological input file with NWS = 20 for more details. As a standard procedure, the and are pre-computed in 4 storm quadrants for all available isotaches in the ASWIP program [footnotes 1] and appended to the input file prior to running an ADCIRC simulation. The following describes the procedures to prepare the input file for the GAHM.
First, the influence of the boundary layer effect must be removed to bring the maximum sustained wind and the 34-, 50-, and/or 64-kt isotaches from 10 meter height to the gradient wind level. Practically, the maximum gradient wind can be directly calculated as
where is the reported maximum sustained wind at 10 meter height assuming in the same direction as , is the storm translational speed calculated from successive storm center locations, is the wind reduction factor for reducing wind speed from the gradient wind level to the surface at 10 meter height (Powell et al., 2003), and is the damp factor for . The following formula of is employed in the ASWIP program:
which is the ratio of gradient wind speed to the maximum wind speed along a radial wind profile. Thus, is zero at storm center, and increases with until reaches a maximum value of 1 at , then gradually decreases outward to zero.
In addition to the scalar reduction in wind speed, surface friction and continuity also cause the vortex wind to flow inward across isobars, with an inward rotation angle according to the Queensland Government's Ocean Hazards Assessment (2001) [4]:
Thus, the gradient wind at the radii to specified storm isotaches in 4 storm quadrants can be obtained from the observed isotaches as
where is the observed isotach wind speed with an unknown angle , and is the wind speed at radius to specified isotach before the inward rotation angle is removed.
Rewriting (17) in x- and y-components yields:
where is the azimuth angle of the storm quadrant (NE, SE, SW, NW at , respectively), and are the zonal and meridional components of , and are the zonal and meridional components of .
Given an initial guess of , values of and can be solved iteratively from (9) and (11) until both converge, and can be estimated by combining (15), (17), (18), and (19). Plugging from (14), the above calculated and the observed radius to back into (13), a new can be inversely solved by a root-finding algorithm. Since the above calculations are carried out based on an initial guess of , wWe need to repeat the entire process until converges.
In case where multiple isotaches are given in the forecast/best track advisories, the for the highest isotach will be calculated using the above procedure, and used as the pseudo for the entire storm (physically, there is only one found along a radial wind profile ). For each lower isotach, will be calculated with the pseudo set as its initial value to determine the inward rotation angle following the above process only once. The use of the pseudo across all storm isotaches ensures that the cross-isobar frictional inflow angle changes smoothly along the radius according to (17).
Occasionally, we have to deal with situations where , which violate (13) so couldn't be calculated. These situations mostly happen in the right hand quadrants (in the Northern Atmosphere) of a weak storm with a relatively high translational speed. For cases like this, we assign , which is equivalent to assigning .
After the ASWIP program finishes processing the input file, it can be readily used by the GAHM to construct spatial pressure and wind fields in ADCIRC for storm surge forecast.
Composite Wind Generation
Since storm parameters are only given in 4 storm quadrants (assuming at azimuthal angles, respectively) at 3 available isotaches in the input file, spatial interpolation of storm parameters must take place first at each ADCIRC grid node. Traditionally, the single-isotach approach is used by the AHM, in which storm parameters will be interpolated azimuthally from the highest isotach only. To take advantage of the availability of multiple isotaches, a new composite wind method is introduced in the GAHM, the multiple-isotach approach, in which storm parameters will be interpolated both azimuthally and radially from all available isotaches.
To begin, the relative location of a node to the storm center at given time is calculated, specified by the azimuth angle and distance . The angle places the node between two adjacent quadrants and , where . For each storm parameter to be interpolated, its value at are weighted between its values at two pseudo nodes and :
The distance then places each pseudo node between the radii of two adjacent isotaches in its quadrant, and the value at the pseudo node is interpolated using the inverse distance weighting (IDW) method:
where are parameter values computed from the 34-, 50-, and 64-isotach, are distance weighting factors for each isotach, calculated as
and .
The above procedure is performed at each node of an ADCIRC grid. After all storm parameters are interpolated, the pressure and gradient winds can be calculated using (12)&(13). To bring the gradient wind down to the standard 10 meter reference level, the same wind reduction factor is applied, and the tangential winds are rotated by an inward flow angle β according to (16). Then, the storm translational speed is added back to the vortex winds. Last but not least, a wind averaging factor is applied to convert resulted wind field from 1-min to 10-min averaged winds in order to be used by ADCIRC. This new composite wind method is simple and efficient, and more importantly, it assures that the constructed surface winds match all observed storm isotaches provided in NHC’s forecast or “best track” advisories.
Case Studies
Preliminary evaluation of the GAHM was carried out based on seven hurricanes that struck the Gulf of Mexico and the Eastern United States: Katrina (2005), Rita (2005), Gustav (2008), Ike (2008), Irene (2011), Isaac (2012), and Sandy (2012), see Table 1. Ranging from category 1 to 5 on the Saffir-Simpson Hurricane Wind Scale, these storms vary in storm track, forward motion, size, intensity, and duration, but all caused severe damages to coastal states due to destructive winds, wind-induced storm surges, and ocean waves. Their “best track” advisories were retrieved from NHC’s ftp site (ftp://ftp.nhc.noaa.gov/atcf; previous years’ data are located in the archive directory) and pre-processed using the ASWIP program. The “best track” file contains an estimate of the radius to the maximum wind for each data entry, but will solely be used for model validation purpose as both the GAHM and AHM calculate their own spatially-varying .
| Hurricane | Saffir-Simpson Wind Scale | Maximum Sustained Wind (knot) | Minimum Central Pressure (mbar) | Period from Formation to Dissipation |
|---|---|---|---|---|
| Katrina | 5 | 150 | 902 | 08/23-08/30, 2005 |
| Rita | 5 | 150 | 902 | 09/18-09/26, 2005 |
| Gustav | 4 | 135 | 941 | 08/23-09/04, 2008 |
| Ike | 4 | 125 | 935 | 09/01-09/14, 2008 |
| Irene | 3 | 105 | 942 | 08/21-08/30, 2011 |
| Isaac | 1 | 70 | 965 | 08/21-09/03, 2012 |
| Sandy | 3 | 95 | 940 | 10/22-10/01, 2012 |
Besides the maximum wind speed, both Holland and can be used as key storm characteristics to characterize the development of the storm. Figure 4 depicts the change of , , and during different stages of the hurricanes along their best tracks. Typically, both and increase as hurricane strengthens, and decrease as hurricane dissipates, within the range of (0, 2.5). Previous analytical evaluation has demonstrated that the GAHM behaves consistently better than the HM, especially under situations where . Here, evaluation of model performance will be carried out by comparing the modeled winds with the observed winds in the "best track" data, as well as the AHM, the SLOSH (Sea, Lake, and Overland Surges from Hurricanes) winds, re-analysis H*Wind and hindcast OWI modeled winds. The OWI winds and H*Winds are considered more mature wind products that are able to resolve more complex structures of a hurricane than the simple vortex models do.

|

|

|
| Figure 4. The development of (a) The Maximum Wind Speed, (b) Holland , and (c) along the best tracks of 7 selected hurricanes | ||
The AHM vs. The GAHM
- Comparison of Radial Wind Profiles using the Single-Isotach Approach
Since the AHM is an advanced version of the HM, here we only use model results from the AHM for comparisons with the GAHM. First, the single-isotach approach was evaluated using Hurricane Irene (2011) as an example. Figure 5 gives the comparison of radial wind profiles of Hurricane Irene (2011) between the AHM and the GAHM using the single-isotach approach at three snapshots, each representing the developing (top panels), mature (middle panels), and dissipating (bottom panels) stages of the hurricane.
The cross-section radial winds from SW to NE are given in the left panels, and NW to SE in the right panels. The observed isotaches at radii to specified isotaches given in the "best track" file are also plotted as vertical line segments for reference (highest isotach in black and lower isotaches in gray). For a perfect match between the modeled winds and the isotaches, the radial profiles should meet the tip of the line segments at the exact same height. The , and are also computed at the same snapshots in all 4 quadrants, given by Table 2.
| 2011-Aug-21 18:00 | 2011-Aug-25 00:00 | 2011-Aug-28 06:00 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quadrant | NE | SE | SE | NW | NE | SE | SW | NW | NE | SE | SW | NW |
| 1.00 | 1.00 | 1.00 | 1.00 | 1.62 | 1.62 | 1.62 | 1.62 | 0.60 | 0.60 | 0.60 | 0.60 | |
| 1.24 | 1.03 | 1.05 | 1.19 | 1.69 | 1.69 | 1.65 | 1.68 | 1.11 | 0.92 | 0.72 | 0.73 | |
| 0.64 | 1.44 | 1.26 | 0.74 | 1.37 | 1.36 | 1.70 | 1.41 | 0.28 | 0.33 | 0.74 | 0.82 | |
It is evident that the radial wind profiles generated by the GAHM consistently match the highest isotaches in all quadrants at different stages of Irene, no matter how and vary. The AHM did a similarly good job when the hurricane is strong (see middle panels), but failed to match the highest isotaches when . Both the AHM and the GAHM winds died off too quickly away from the storm center, thus failed to match any lower isotaches.
- Evaluation of the Maximum Winds and Radius to Maximum Winds
Comparisons of the modeled maximum winds and radius to maximum winds to the observed values in the input file were also carried out based on all 7 selected hurricanes, given by the scatter plots in Figure 6. Evaluations of the maximum winds are given in the upper panels, while the radius to maximum winds given in lower panels, both color-coded by , with a simple linear correlation given in each panel. Examination of the upper panels reveals that the GAHM did an excellent job in estimating the maximum winds, with a few overestimations near the lower bound of the dataset. Careful examinations of these over estimated values revealed that they were from those "bad" dada entries in the "best track" file that violate certain criteria in the GAHM when solving for the . This phenomenon was particular common during the dissipating stage of a hurricane. The AHM had larger discrepancies in estimating the maximum wind compared to the GAHM, especially when , which was a direct consequence of the cyclostrophic balance assumption made during the derivation of HM's equations. Examination of the lower panels reveals that the maximum value of the modeled azimuthally-varying failed to match the observed values given in the input file, but the trend of the GAHM was significantly better.

|

|
| Figure 6. Comparison of the modeled and “Best Track” maximum winds (upper two panels), and the modeled and “Best Track” (lower two panels) between the AHM and the GAHM based on all seven hurricanes. |
- Demonstration of the Multiple-Isotach Approach
Earlier we have shown that a radial wind profile constructed by the GAHM using the single-isotach approach would only match the highest isotach, due to limitations of this single-fitting method. In fact, underestimations of modeled winds at distances to isotachs other than the highest one were common, as the radial wind profile tends to die off too quickly away from the storm center due to the nature of GAHM’s formulas. In an effort to minimize the combined errors mentioned above, and to improve the overall accuracy of the estimated wind field, the multiple-isotach approach should be used whenever there is more than one isotach present in the best track file.
The 3D plots of Irene’s radial wind profiles (left) and interpolated spatial wind fields (right) by the GAHM using the single-isotach approach (upper panels) versus the multiple-isotach approach (lower panels) were given by Figure 7. For easier visualization, all available isotaches were plotted at radii to specified isotaches in the left two panels, and as contour lines (after azimuthal interpolation) in the right two panels. It is evident that winds generated by the multiple-isotach approach were able to match all given isotaches in all 4 quadrants, while only the highest isotach was matched by the single-isotach approach. Comparison of the spatial wind fields also indicated that the multiple-isotach approach allowed the wind to die off more gradually away from the storm center than the single-isotach approach did, demonstrated by the smaller gradient of the contour lines in the lower panel. It is believed that the multiple-isotach approach improves the overall accuracy and performance of the GAHM.
Evaluation of GAHM's Composite Wind Field
- Comparison of Radial Wind Profiles
Using the multiple-isotach approach, radial wind profiles generated from the GAHM were compared to those from the AHM, the SLOSH, H*Winds, and OWI winds, shown in Figure 8 at three different stages of Irene (2011), with the left panels showing the SW to NE cross-section winds, and the right showing the NW to SE cross-section winds (same as in Figure 5). It is evident that the GAHM's composite radial wind profiles matched all available storm isotachs at all time, while the rest of the models failed most of the time. The SLOSH model, which is also a parametric wind model, does not take the isotach information to construct its wind field, so generally did a bad job matching any given isotaches. More detailed wind structures can be observed from the radial profiles extracted from the H*Wind and OWI winds than those from the parametric wind profiles, as expected. However, profiles from different models in general did not match each other due to different mechanisms involved in each model.
- Evaluation of Model Results at Radii to Given Isotaches
Quantitative evaluation of the GAHM's performance at radii to given isotaches were given in Figure 9, with statistics given in Table 3, based on all seven selected hurricanes. The GAHM had almost perfect match to each of the 34-, 50-, and 64-kt isotaches, with a standard deviation around 0.1 kt, which was very impressive. The AHM matched the 64-kt isotach reasonably well with a mean of 63.3 kts, but failed at the lower isotaches. The SLOSH did not take any isotach information to construct its wind fields, thus behaved poorly in matching any given isotaches. Its data also had the largest spread compared to other models, with standard deviation ranging from 11 to 16 kts. For the H*Wind and the OWI winds, the means of modeled winds were close to each specified isotach, generally within ±3 kts, but the spreads of data were also large compared to that of the AHM and the GAHM, with a standard deviation greater than 7 kts.
| MEAN (kt) | Standard Deviation (kt) | |||||
|---|---|---|---|---|---|---|
| Iso-34 | Iso-50 | Iso-64 | Iso-34 | Iso-50 | Iso-64 | |
| AHM | 26.9 | 44.7 | 63.3 | 7.96 | 7.09 | 2.55 |
| GAHM | 34.0 | 50.0 | 64.0 | 0.10 | 0.12 | 0.10 |
| SLOSH | 30.0 | 48.9 | 69.5 | 11.00 | 14.11 | 16.08 |
| OWI | 33.1 | 48.3 | 61.3 | 7.65 | 8.71 | 9.42 |
| H*Wind | 34.9 | 49.2 | 61.2 | 7.55 | 8.88 | 8.89 |
- Comparison of Spatial Wind fields
Comparisons of spatial wind fields among the AHM, the GAHM using the multiple-isotach approach, the SLOSH, H*Wind and OWI winds (in rows) were given by Figure 10 at the same snapshots (in columns) as in Figure 8. The 34-, 50-, and 64-kt contour lines were shown in each wind snapshot. In general, the AHM and GAHM winds shared a lot of similarities. During weaker periods of Irene, the differences between the AHM and the GAHM's spatial wind fields were mostly observed in the inner region of the hurricane due to differences in calculated . More specifically, the calculated in the AHM was under-predicted (thus is closer to the storm center) than that in the GAHM, resulted from the faulty cyclostrophic balance assumption made in the HM and AHM. During stronger periods of Irene, however, the differences were mostly observed in the outer region of the hurricane due to the usage of the multiple-isotach approach in the GAHM. Without taking into account storm information from lower isotaches, the AHM winds tended to die off too quickly away from the storm center. The SLOSH winds did not show much similarity to the AHM and GAHM winds. It used an azimuthally constant from the "best track" file to generate its vortex winds, and a distance-weighted translational speed to account for storm asymmetry, which was not rendered properly when the storm was strong. The winds fields of H*Wind and OWI winds were much more complex than those of the simple parametric models, but the GAHM did a relatively good job matching the spatial patterns of the hurricane. Although it is unlikely that the parametric winds constructed over a minimum set of data would match the level of details and complexity in the re-analysis H*Wind and the numerical OWI winds, the ability of a the GAHM to produce reasonable estimates of surface wind fields in a timely manner was highly desirable for real-time forecasting.
Notes
- ↑ The auxiliary preprocessing program ASWIP.F (located in the /wind directory) was further developed here to accommodate the GAHM.
References
- ↑ Holland, G. J., 1980: An analytic model of the wind and pressure profiles in hurricanes. Monthly Weather Review, 108, 1212-1218.
- ↑ Mattocks, C., C. Forbes, and L. Ran, 2006: Design and implementation of a real-time storm surge and flood forecasting capability for the State of North Carolina. UNC-CEP Technical Report, University of North Carolina, 103pp.
- ↑ Powell, Mark & Uhlhorn, E. & Kepert, Jeffrey. (2009). Estimating Maximum Surface Winds from Hurricane Reconnaissance Measurements. Weather and Forecasting. 24. 10.1175/2008WAF2007087.1.
- ↑ Queensland Government, 2011: Queensland Climate Change and Community Vulnerability to Tropical Cyclone, Ocean Hazards Assessment – Stage 1.